التركيب النووي
تتكون نواة ذرة ذات عدد ذري ![]() وعدد كتلي
وعدد كتلي ![]() من عدد من البروتونات
من عدد من البروتونات ![]() وعدد من النترونات
وعدد من النترونات ![]() . تتميز جميع الذرات تقريباً بكتل ذرية ذات عدد صحيح، ويمثل
. تتميز جميع الذرات تقريباً بكتل ذرية ذات عدد صحيح، ويمثل ![]() العدد الكلي للنكليونات (نترونات وبروتونات) في النواة.
العدد الكلي للنكليونات (نترونات وبروتونات) في النواة.
يحدد العدد الذري ![]() العنصر الكيميائي، ونعرف أكثر من
العنصر الكيميائي، ونعرف أكثر من ![]() عنصر كيميائي، كما يمكن لنوى العنصر الواحد أن تمتلك أعداداً كتلية متباينة، ومعلوم لنا أكثر من
عنصر كيميائي، كما يمكن لنوى العنصر الواحد أن تمتلك أعداداً كتلية متباينة، ومعلوم لنا أكثر من ![]() نوعاً من النوى يدعى كل منها بالنكليد، وهي الذرات المصنفة بحسب قيم العدد الذري
نوعاً من النوى يدعى كل منها بالنكليد، وهي الذرات المصنفة بحسب قيم العدد الذري ![]() والعدد الكتلي
والعدد الكتلي ![]() (أو عدد النترونات) معاً. وتم تصميم كتابة الرمز الكيميائي بوضع العدد الذري
(أو عدد النترونات) معاً. وتم تصميم كتابة الرمز الكيميائي بوضع العدد الذري ![]() في أسفل ويسار الرمز أما العدد الكتلي
في أسفل ويسار الرمز أما العدد الكتلي ![]() في أعلى ويسار الرمز
في أعلى ويسار الرمز ![]() . مثال، جميع ما يلي هي نكليدات:
. مثال، جميع ما يلي هي نكليدات: ![]() ،
، ![]() ،
، ![]() ،
، ![]() .
.
تعرف النكليدات التي تضم العدد نفسه من البروتونات (أي التي تنتمي إلى العنصر الكيميائي نفسه) ولكن أعداد مختلفة من النترونات بالنظائر Isotopes. مثال: ![]() ،
، ![]() ،
، ![]() . وتعرف النكليدات التي تملك نفس عدد النترونات بالإيزوتونات Isotones. مثال:
. وتعرف النكليدات التي تملك نفس عدد النترونات بالإيزوتونات Isotones. مثال: ![]() ،
، ![]() كلتا الذرتين تملكان عدد من النترونات يساوي
كلتا الذرتين تملكان عدد من النترونات يساوي ![]() .
.
ذكرنا سابقاً أن لذرة الهيدروجين ثلاثة نظائر طبيعية حيث أن الهيدروجين والديتيريوم نكليدات مستقرة أما التريتيوم فهو نكليد مشع. ولعنصر الفلور نظير واحد طبيعي ![]() أما باقي نظائره فهي صنعية مشعة ذات عمر قصير. تعكس الأوزان الذرية المقاسة للعناصر الوفرة النسبية للنظائر الطبيعية كما هو موضح في المثال التالي.
أما باقي نظائره فهي صنعية مشعة ذات عمر قصير. تعكس الأوزان الذرية المقاسة للعناصر الوفرة النسبية للنظائر الطبيعية كما هو موضح في المثال التالي.
مثـــال
وُجد أن لعنصر الكلور في الطبيعة نظيرين، الأول ![]() بوفرة %
بوفرة %![]() ، والثاني
، والثاني ![]() بوفرة %
بوفرة %![]() . ويبلغ الوزن الذري لكل من النظيرين
. ويبلغ الوزن الذري لكل من النظيرين ![]() و
و ![]() على الترتيب. أحسب الوزن الذري الملاحظ لعنصر الكلور.
على الترتيب. أحسب الوزن الذري الملاحظ لعنصر الكلور.
الحـــــل
لحساب الوزن الذري لعنصر الكلور نقوم بجمع الوزن الذري للنظيربن، كُلٌ بحسب نسبة وفرته في الطبيعة:
![]()
تتميز نظائر أي عنصر كيميائي بأن لها نفس التكوين الإلكتروني، ولهذا لا يمكن فصلها كيميائياً. كما يسبب وجود النظائر اضطراباً صغيراً جداً في مستويات الطاقة الذرية مما يؤدي لملاحظة انزياح النظير في بعض الخطوط الطيفية. يسبب اختلاف السبينات النووية (العزوم الذاتية) للنظائر المختلفة تبايناً في التركيب فائق الدقة في أطياف العناصر، ولوجود النظائر في الطبيعة أثرٌ كبيرٌ على أطياف الجزيئات (دورانياً واهتزازياً).
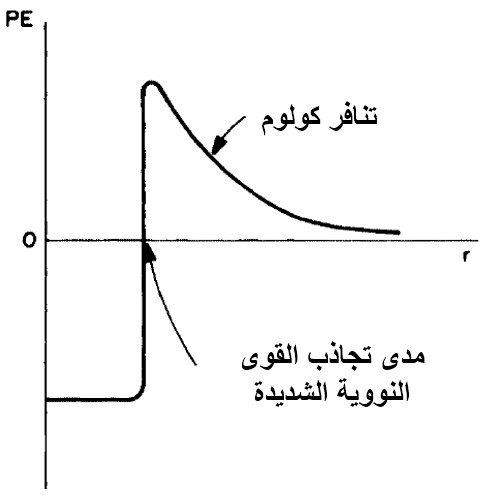
ترتبط النكليونات مع بعضها البعض في النواة بتأثير القوة النووية الشديدة، يساوي مدى هذه القوة في الحدود النووية تقريباً ![]() وهي شديدة لدرجة كافية تجعلها تطغى على قوة كولوم التنافرية بين بروتونين ضمن النواة. يبين المخطط (أ) التالي الطاقة الكامنة لبروتون كتابع للمسافة
وهي شديدة لدرجة كافية تجعلها تطغى على قوة كولوم التنافرية بين بروتونين ضمن النواة. يبين المخطط (أ) التالي الطاقة الكامنة لبروتون كتابع للمسافة ![]() بين مركزه ومركز النواة.
بين مركزه ومركز النواة.
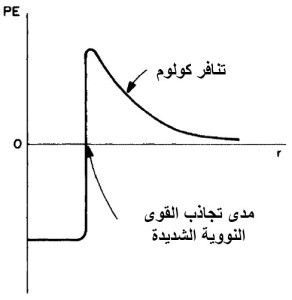
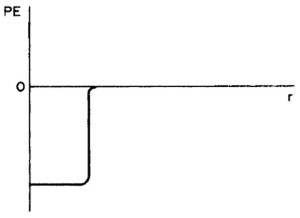
عند مسافات كبيرة فاصلة بين البروتون والنواة تسعى الطاقة الكامنة للصفر، وعندما يقترب تزداد طاقته الكامنة بسبب قوة كولوم التنافرية بين الشحنتين الموجبتين. وباقترابه أكثر من النواة ودخوله ضمن مجال جذب القوة النووية الشديدة، تتحول طاقته الكامنة فجأةً إلى مقدار سالب ويمكنه التفاعل مع النواة. في شروط معينة، يمكن أن تتحول الطاقة الكلية للبروتون إلى مقدار سالب وتشغل عندها حالة ارتباط ضمن النواة. يحتاج الجسيم المشحون إيجابياً، كما نعلم، لطاقة كبيرة لكي يستطيع الاقتراب من النواة، بينما يمكن للنترون الولوج إلى النواة مهما كانت طاقته، لغياب حاجز كولوم أمامه كونه جسيم عديم الشحنة. يوضح المخطط (ب) منحني الطاقة الكامنة لنترون ونواة.
مثـــال
ما هي أقل طاقة يمكن أن يملكها بروتون ليتفاعل مع نواة ذرة الكلور الساكنة؟
الحـــل
بالعودة للمخطط (أ)، ينبغي على البروتون أن يملك طاقة كافية ليعبر الحاجز الكولومي التنافري عند التصادم. يمكن أن تسمح له هذه الطاقة بالوصول إلى النواة الهدف. ولحساب أنصاف أقطار كل من البروتون ونواة الكلور وكيف يتباعد مركزيهما نستخدم المعادلة ![]() ، ونعلم أن
، ونعلم أن ![]() و
و ![]() ، وبالتعويض بالمعادلة السابقة نجد:
، وبالتعويض بالمعادلة السابقة نجد:
![]()
![]()
للبروتون الشحنة الأحادية الموجبة ![]() وللكلور
وللكلور ![]() الشحنة
الشحنة ![]() . وتكون الطاقة الكامنة لهاتين الشحنتين اللتين تفصل بينهما المسافة
. وتكون الطاقة الكامنة لهاتين الشحنتين اللتين تفصل بينهما المسافة ![]() تساوي إلى:
تساوي إلى:
![]()
![]()
كما هي الذرة كذلك النواة أيضاً، هي نظام ميكانيكي كمومي من الجسيمات المترابطة. تتفاعل النكليونات فيما بينها ضمن النواة بالقوى النووية الشديدة وهي قوة أكثر تعقيداً من القوة الكهرومغناطيسية التي تحكم تركيب وخواص الذرات والجزيئات. ولكن لا يمكن لمعادلات الموجة التي تصف النواة أن تحل بنفس درجة الدقة التي تحل بها معادلات الموجة الذرية، ولكن العديد من الخواص المفصلة للنواة قد تم حلها واختبارها بالتجربة. يملك كل من النترون والبروتون سبين (عزم ذاتي) يساوي ![]() وبالتالي يتبعان مبدأ الاستبعاد لباولي. وكما يوجد أيضاً حالة مثارة للإلكترونات الذرية، يمكن أن تملك النواة أيضاً حالة مثارة، ولكن تتميز الذرة بامتلاكها عدد لا منتهي من حالات الارتباط المثارة، بينما للنواة عدد محدود. ويعزى هذا الاختلاف بين التركيب الذري والنووي إلى المدى اللامنتهي من قوة كولوم بخلاف المدى القصير والمحدود للقوة النووية الشديدة.
وبالتالي يتبعان مبدأ الاستبعاد لباولي. وكما يوجد أيضاً حالة مثارة للإلكترونات الذرية، يمكن أن تملك النواة أيضاً حالة مثارة، ولكن تتميز الذرة بامتلاكها عدد لا منتهي من حالات الارتباط المثارة، بينما للنواة عدد محدود. ويعزى هذا الاختلاف بين التركيب الذري والنووي إلى المدى اللامنتهي من قوة كولوم بخلاف المدى القصير والمحدود للقوة النووية الشديدة.
يظهر مخطط سويات الطاقة لنواة ![]() في الشكل (ج) أن نواة الليثيوم تملك عدداً من حالات الارتباط المثارة، ويلاحظ أن السوية
في الشكل (ج) أن نواة الليثيوم تملك عدداً من حالات الارتباط المثارة، ويلاحظ أن السوية ![]() لها عمر قصير جداً ولذلك لا تملك طاقة محددة بشكل حاد.
لها عمر قصير جداً ولذلك لا تملك طاقة محددة بشكل حاد.

إن كل من الديتيريوم وجسيم ألفا (نواة ![]() و
و ![]() ) هي أمثلة على النوى التي لا تملك حالة ارتباط مثارة.
) هي أمثلة على النوى التي لا تملك حالة ارتباط مثارة.
المرجع: Atoms, Radiation and Radiation Protection James E. Turner
ترجمه بتصرف: سامر عبد الرزاق بكر